World Models on the Pareto Frontier
Recognize trade-offs through graphs!
This essay is a guest post from the geometer Christopher Sheldon-Dante.
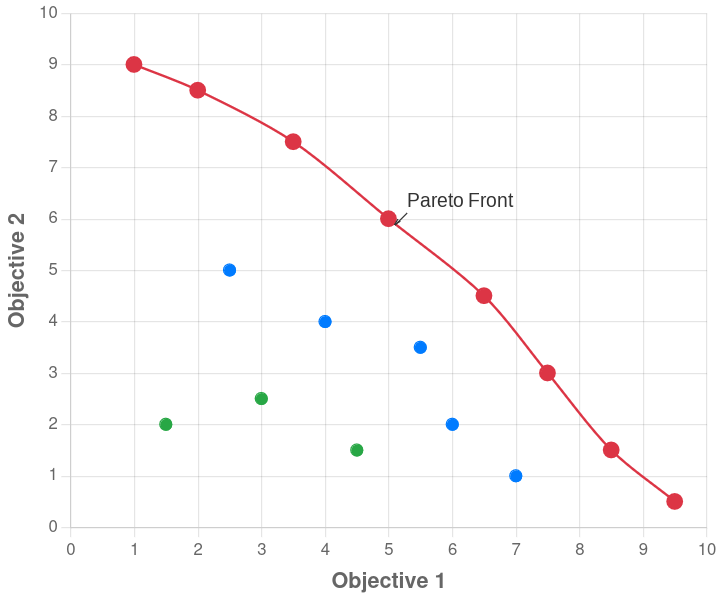
In every field, there are competing models that seem to subtly contradict each other yet each illuminate different aspects of reality. It’s easy to become a partisan, holding one framework in high esteem and defending it against its competitors. But there are ways to hold competing ideas without feeling a need to choose a single winner. One such way is to arrange these models on a Pareto frontier defined by objective metrics like compression and prediction, then keep everything that isn't strictly worse than another entry.
The Pareto frontier concept is simple: plot all solutions where improving one dimension requires sacrificing another. A complex but accurate model and a simple but imprecise one might both deserve spots if neither is clearly better. This approach is useful across domains, from comparing theories of mind to theories of physics. It preserves multiple valid approaches rather than demanding we choose a single winner. The concept originates from economics, where it's used to map optimal trade-offs between risk and reward—no portfolio can increase expected returns without accepting more risk, so all efficient portfolios live on the frontier.
The Engine of Understanding
Knowledge-building is fundamentally about pattern recognition. All knowledge starts from what we directly experience. We notice patterns and regularities, then build models to capture them. Some philosophers worry about whether induction is justified, but we can sidestep that debate: we'll use whatever models help us predict what comes next. These models stick around if they're useful.
Our human minds come equipped with remarkable tools for this project, such as language, mathematics, logic, probability theory. These tools let us translate messy observations into symbolic models that we can manipulate, test, and systematically compare.
Once you have multiple symbolic models, you must begin to choose between them. Using a Pareto frontier prevents us from having to choose arbitrarily. Choose the metrics for what you value, and compare models across all of them. This can include rigorously defined metrics like MDL compression alongside subjective preferences like personal taste. All that is needed is a transitive ordering along each parameter we care about.
The frontier reveals all models that aren't dominated—each representing a different optimal trade-off across your chosen criteria. This approach lets you discard clearly inferior models while preserving flexibility: you don't have to pick a single "winner" from the frontier, since your final choice can depend on personal preferences or specific contextual needs.
Doing this lets us share and evaluate our models across shared criteria with others. You don’t necessarily share my subjective preferences in your epistemology, but when we compare our favored models my preferred models may become dominated by dropping that preference. We then gain a common language for comparing models so we can debate merit across agreed upon metrics and ignore preference components that are not aligned.
How to Evaluate Competing Models
What dimensions actually matter for model evaluation?
Predictive accuracy: How often does the model get things right?
Compression ratio: How much data can you explain with how little theory?
Predictive precision: How specific are the model's forecasts?
Computational efficiency: How much effort does it take to use the model?
Robustness: How well does it generalize to new situations?
Interpretability: Can you understand why it makes the predictions it does?
Complexity and Parsimony
All models are wrong, but some are useful — E.P. Box
The above metrics are suggested because scoring well on them generally makes a model more useful to us. This is straightforward for things like accuracy, precision and robustness which correspond with intuitive concepts of correctness. It's also not too hard to see how computational efficiency and ineterpretability relate to how easy a model is to work with and communicate about. However, compression stands out as a bit less intuitive than the rest and it is arguably a single materic that most completely fromalizes and captures what people mean when they say they "understand" something.
A lot of the above metrics seem to be focused on prediction, but human understanding often focuses on past observations. It is common for people to say "that fits" or "that makes sense" when evaluating knowledge in the context of their internal mental models. Likewise, mental models that don't generalize well to future data are often also considered at best incomplete. Effectively when we have a good understanding of something it lets past observations make sense and future events become predictable—you minimize surprises.
High compression captures this: instead of storing every individual data point, you have a compact theory that generates the data. It's the difference between memorizing astronomical tables and knowing the equations that predict planetary motion. We have some data about the world, and our world models help us hold onto that data with a smaller footprint in memory overall while also predicting future data accurately.
That is to say that we seek to minimize the size of the model plus the size of the residual data. What's more, because compression includes the model size in its measure, it prioritizes models that are simpler and gets rid of structure that does not improve accuracy. This aligns with both the desire to have more interpretable models (less to think about) and more computationally efficient models (less to reason about).
Many formal theories exist to quantify this, such as minimum description length or Kolmogorov complexity. Although I use the word “quantify” somewhat loosely, as Kolmogorov complexity is generally regarded as incomputable, and MDL depends on the choice of encoding. Regardless of the specifics, compression stands out as a particularly salient metric for our pareto frontier in terms of its ability to capture many things we care about such as accuracy, robustness and interpretability in a single metric.
Meta Modeling, this Idea on the Pareto Front
I recommend that when you’re comparing models, you should choose the epistemic values, such as precision or compression, somewhat subjectively, and partially as a matter of taste. But that raises a natural question: if we're choosing how to evaluate models, how do we evaluate our method of evaluation?
This entire epistemological framework is itself considered a model residing on the Pareto frontier of possible epistemologies. It is not presented as a final, immutable truth but as a current "best candidate" methodology for inquiry, subject to its own principles of evaluation and revision.
This creates something remarkable: a methodology that can discover better methodologies. The framework provides tools for evaluating and potentially replacing itself, creating a self-improving system that guards against intellectual stagnation. Thus, we can place this own model of Pareto frontiers in the context of other epistemic comparisons, in a meta fashion.
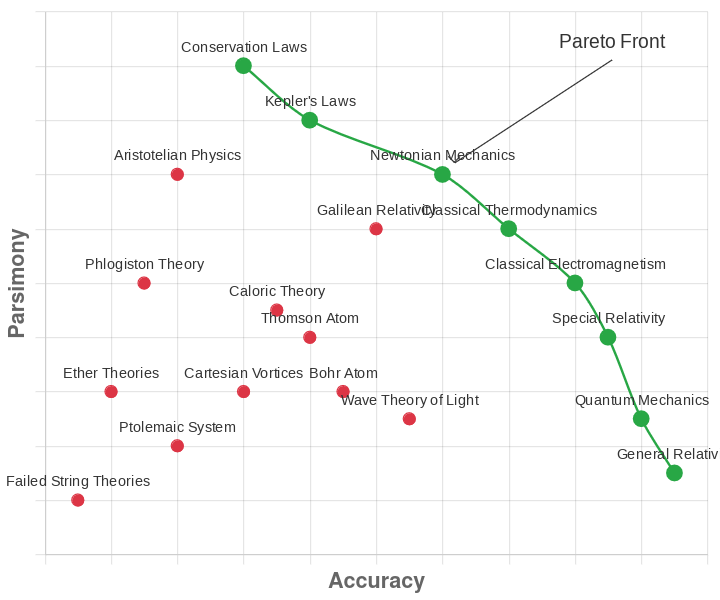
Examples
It is through the application of the methodology that specific ontological models — such as those arising in physics, logic, or computation — instantiate claims about the nature of entities and their interactions. These models can then be evaluated according to their predictive success, compression power, precision, generality across subjective experience, and so on. This gives us a powerful way to identify salient ontological features of reality within our current epistemic limits. Our frontier models, and more specifically the entities they postulate, represent our best descriptions of what exists.
Contemporary physicalist models succeed in describing large swaths of subjective experience by postulating coherent groupings like particles, fields, or wavefunctions that compress observed interactions efficiently. These groupings are not assumed a priori, but are retained because they are part of models that dominate along the Pareto frontier described by our methodology. Thus, particle-like entities earn their ontological status because they are part of one of our best descriptions of subjective experience: they allow us to organize and predict experience compactly.
Just as with questions of existence, theories of consciousness get evaluated on the Pareto frontier. Physicalist models of mind dominate, at least for me, because they offer the most parsimonious and predictively powerful explanations for cognitive phenomena. Instead of endless debates between dualists and physicalists about the "hard problem" of consciousness, the frontier approach transforms this into an empirical question: which models compress the most data about cognitive phenomena while making the most accurate predictions?
In the End
I hope this changes your own thinking. Don’t commit to single theories about complex topics, and instead maintain a portfolio of models that excel in different dimensions. If consciousness seems mysterious, then keep multiple approaches, computational, phenomenological, or neurological, and use whichever of them performs best for your current question. Sometimes one mental model is strictly better than its competitor, but usually the difference reflects a tradeoff. Recognize the tradeoff, and hold both sides of it in mind!